说一个代码简单的做法。本题解数形结合,容易理解。
题解

首先,题目所求就是上述不等式对哪个 $i$ 成立。
发现式中只有第 $2$ 项是随着 $i$ 而变化的。而第 $1$ 项虽然不变,但是较为复杂,与第 $2$ 项相减的结果不好快速计算,因此不妨将第 $2$ 项移项到右边。

是不是突然发现这下不等式两边都比较简单了?如果看不出来,我们不妨把式子左右的图叠在一起看:
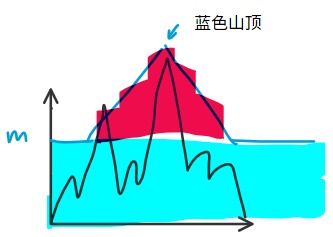
下文中称 $(x_i,p_i+m)$ 点为蓝色山顶(图中标出)
我们考虑右边能把左边盖住的条件:
- 对于左边高度小于等于 $m$ 的点,显然不用考虑
- 对于左边高度大于 $m$ 的某一点,蓝色山顶必须位于下图红色阴影区域内:
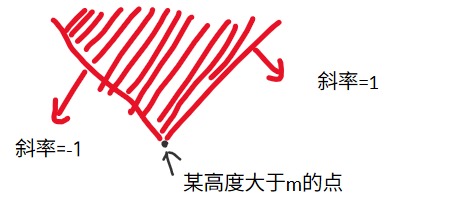
显然,只要左边的所有极值点都满足上述条件,那么左边的所有点都满足上述条件。到了这里,做法就显而易见了。我们只需要枚举所有左侧的极值点,然后把他们的红色阴影区域求交,再判断某个 $i$ 对应的蓝色山顶是否在这个区域内即可。
至于维护红色阴影的交,可以把这个区域看成两个斜率分别为 $\pm1$ 的一次函数取 max,因此求交的时候只需要对应截距取 max 即可。
剩下的就是一些简单的技术问题,比如离散化,差分,不再赘述。
复杂度 $O(n\log n)$,瓶颈在离散化。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
|
#include <bits/stdc++.h>
using namespace std;
#define fi first
#define se second
using ll = long long;
void umx(ll &x, const ll &y) { x = max(x, y); }
const char nl = '\n';
const ll INF = 1e18;
const ll MXN = 1e6 + 5;
ll n, m;
map<ll, ll> delt;
ll x[MXN], p[MXN];
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
int t;
cin >> t;
while (t--) {
delt.clear();
cin >> n >> m;
for (ll i = 1; i <= n; i++) {
cin >> x[i] >> p[i];
delt[x[i] - p[i] + 1]++;
delt[x[i] + 1] -= 2;
delt[x[i] + p[i] + 1]++;
}
ll b = 0, k = 0, lastx = -INF;
ll b_1 = -INF, b1 = -INF;
for (auto it : delt) {
b += k * (it.fi - lastx);
k += it.se;
if (b > m) {
umx(b1, b - it.fi + 1);
umx(b_1, b + it.fi - 1);
}
lastx = it.fi;
}
for (ll i = 1; i <= n; i++) cout << ((p[i] + m - x[i] >= b1) && (p[i] + m + x[i] >= b_1));
cout << nl;
}
return 0;
}
|



