算法

PKUSC2021题解

T1T2

一棵树

题意

题意

题解

$k=0$ 不难，略。

一个显然的想法是枚举断掉的边，然后看每条边的贡献。

贡献分为两类，一类是新加的边的块间贡献:

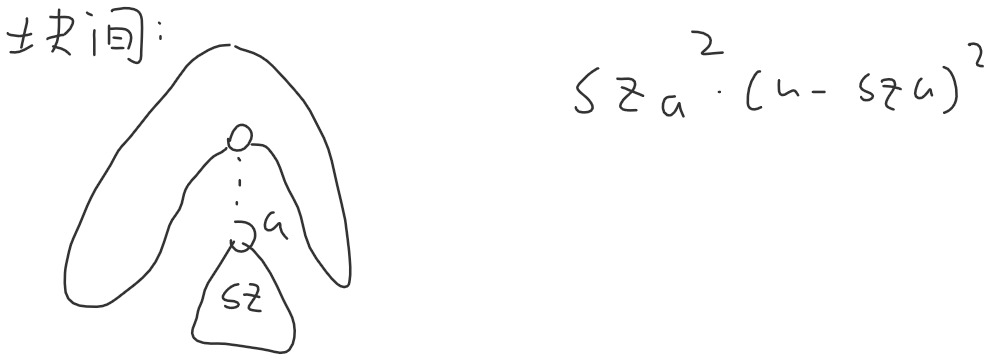
这个不难算，另外一类是原先的边的块内贡献。

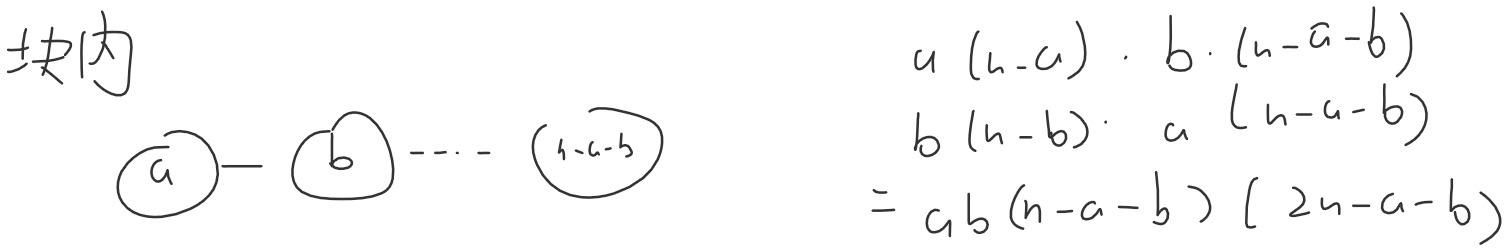
不妨设虚线边断开，实线边把一个连通块分为大小为 $a,b$ 的两块，则这条实线边的贡献是上面的式子。

于是在枚举了虚线边之后，分子树内，祖先，既非子树也非祖先三种情况讨论，不妨设 a 是虚线边较深的端点，b 是实线边较深的端点：

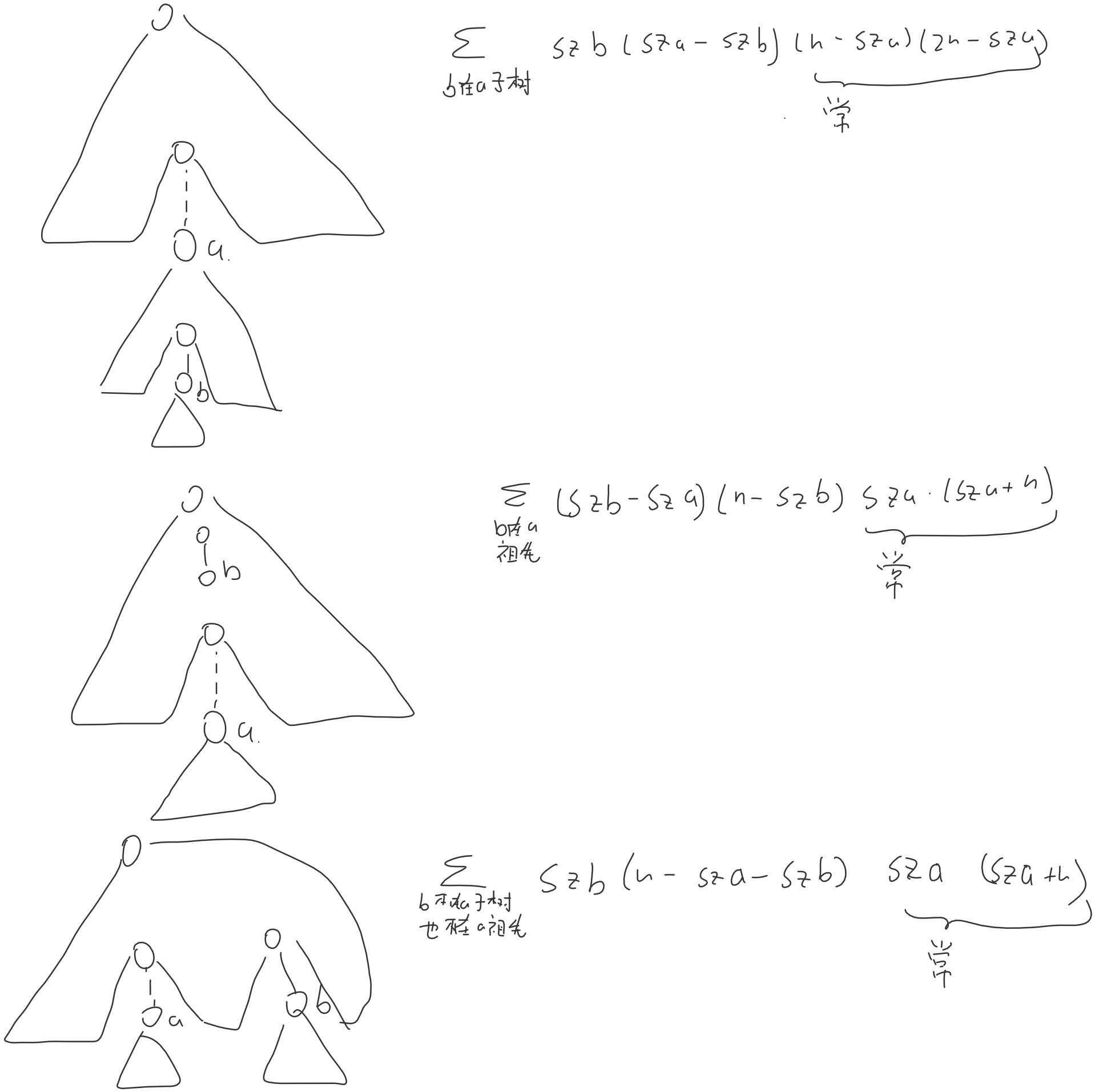
可以发现，三个贡献的式子后两项都只和 a 有关，前两项都可以展开成和 b 有关的二次多项式，因此只需要维护下子树内，祖先上的 sz 的和，sz 的平方之和即可快速计算。

代金券题解

题意

题面

与值域无关做法——贪心

做如下的一个转化，可以看成有三种操作：

  1. 支付 1 个代金券
  2. 支付 1 块钱，不获得代金券
  3. 支付 c 块钱，获得一个代金券

记 $X_i$ 表示第 $i$ 道菜进行操作 1 的次数，$Y_i$ 表示进行操作 3 的次数。

用最少的钱等价于用最多的代金券。因此最优解有如下性质：

  1. 有代金券时不会进行操作 2（代金券越靠前使用越好，否则后面可能没机会用了）
  2. 3 操作必定越靠前越好（感性理解是提前获得了代金券，使用的机会更多了）：

下面是一种调整方法：

$$ Y_i=\lfloor \frac{A_i}c\rfloor, X_i=\min(R_{i-1},A_i\bmod c), R_i=R_{i-1}+Y_i-X_i $$

但是，我们知道，满足这个贪心策略的仅仅是一个前缀，那么这个贪心策略进行到哪里呢？

记 $S_i=\sum_{j\ge i} A_j$，表示 $i$ 后面菜的价值之和。

我们发现：当 $R_i\ge S_{i+1}$ 的时候，就没有必要再进行操作 3 了，因为此时 $i$ 后面后面都可以全用代金券买了。

同时，不难发现满足 $R_i\ge S_{i+1}$ 的 $i$ 是一个后缀。而我们必然在满足这一个条件的第一个 $i$ 就结束了贪心。所以，如果我们能快速判断某个位置是否符合上述条件，我们就能二分求出 $i$ 的位置。

此时我们可能还有一些代金券没有用上，所以我们还需要重新规划第 $i$ 道菜的策略。 首先：

  • 如果 $R_{i-1}
  • 如果 $R_{i-1}>S_{i+1}$，那么就可以把多出来的 $R_{i-1}-S_{i+1}$ 张券在第 $i$ 道菜上用掉。

此时，$i$ 后面花的 $S_{i+1}$ 个券分为两类：第 1 类来自于 $R_{i-1}$，第 2 类来自于 ${Y_i}$。第 1 类券我们可以把它移到第 $i$ 道菜上用，但是第 2 类不可以。

思考一下，还什么方法可能用更多的券？只能增大 $Y_i$，产生一个 2 类券，代替 $S_{i+1}$ 中某个 1 类券的位置，然后再把这个 1 类券移到第 $i$ 道菜上使用。

不妨设 $S_{i+1}$ 中有 $C$ 个 1 类券，第 $i$ 道菜还剩下 $Z$ 块钱没付。那么我们最多能进行 $\min(C,\lfloor \frac Z{c+1}\rfloor)$ 次上述操作。

复杂度 $O(qn)$，拼几个特殊性质，就能喜提 50 左右的好成绩。

上数据结构

难点在于在修改过程中维护 $R_i$，当时考场上就是没想出来这个，就寄了。官方题解中没太搞懂，网上找到一种硬维护的做法。

线段树节点上记三个数 $div,mod,use$ 分别表示区间内所有数除 $c$ 下取整之和（也就是能产生的代金券个数），模 $c$ 之和（也就是最多能使用的代金券个数），以及在初始没有代金券的情况下用贪心策略，会用掉几个代金券。

然后你神奇的发现，这个东西是可以合并的：

1
2
3

node operator+(const node &x, const node &y) {
    return {x.div + y.div, x.mod + y.mod, x.use + y.use + min(y.mod - y.use, x.div - x.use)};
}

前两项显然，解释下第三项咋合并的，x.use + y.use 也是显然的，而 min(y.mod - y.use, x.div - x.use) 表示左边一半用剩下的代金券数量，和右边一半最多能使用的代金券个数取 min。

于是线段树二分即可。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const char nl = '\n';
const ll MXN = 3e5 + 5;
ll n, m, c, tot, sum[MXN];

struct node {
    // /c之和，%c之和，如果在当前区间上模拟，会用掉多少代金券
    ll div, mod, use;
} t[MXN << 2];
node operator+(const node &x, const node &y) {
    return {x.div + y.div, x.mod + y.mod, x.use + y.use + min(y.mod - y.use, x.div - x.use)};
}
#define ls p << 1
#define rs p << 1 | 1
void mdf(ll mi, ll mv, ll p = 1, ll l = 1, ll r = n) {
    if (l == r) {
        tot = tot - (t[p].div * c + t[p].mod) + mv;
        t[p] = {mv / c, mv % c, 0};
        return;
    }
    ll mid = (l + r) >> 1;
    if (mi <= mid)
        mdf(mi, mv, ls, l, mid);
    else
        mdf(mi, mv, rs, mid + 1, r);
    t[p] = t[ls] + t[rs];
}
ll que(ll p = 1, ll l = 1, ll r = n, node lft = {0, 0, 0}, ll rht = 0) {
    if (l == r) {
        ll arr = t[p].div * c + t[p].mod, cur = lft.div - lft.use, ans = lft.use;
        if (cur >= rht) {
            ans += cur, cur -= rht, arr -= cur;
            ans += min(arr / (c + 1), rht);
        } else {
            arr -= c * (rht - cur);
            ans += rht + min(arr / (c + 1), cur);
        }
        return tot - ans;
    }
    ll mid = (l + r) >> 1;
    node _lft = lft + t[ls];
    ll _rht = rht + t[rs].div * c + t[rs].mod;
    if (_lft.div - _lft.use >= _rht)
        return que(ls, l, mid, lft, _rht);
    else
        return que(rs, mid + 1, r, _lft, rht);
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    cin >> n >> m >> c;
    for (ll i = 1, x; i <= n; i++) {
        cin >> x;
        mdf(i, x);
    }
    cout << que() << nl;
    while (m--) {
        ll x, y;
        cin >> x >> y;
        mdf(x, y);
        cout << que() << nl;
    }
    return 0;
}